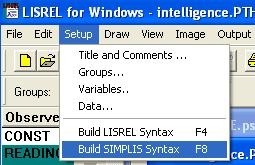
آموزش نحوه ساخت syntax با لیزرل (LISREL)
پراچر (2006)[1]
- ساخت syntax برای برای محاسبه همبستگی بین X و Y:
TI bivariate correlation
DA NI=2 NO=40
CM
0.958365
0.231046 1.163310
MO NX=2 NK=2 LX=DI,FR PH=ST TD=ZE
LK
X Y
ST .5 LX 1 1 LX 2 2 PH 2 1
PD
OU ME=ML ND=4 XM EP=0.00001 IT=1000 NS AD=OFF
- ساخت syntax برای محاسبه همبستگی بین X و Y به طور همزمان در دو گروه، با محدودیت برابری در محل.
- ساخت syntax برای محاسبه همبستگی نسبی بین X و Y، و متغیر کنترل برای هر دو W.
- برای محاسبه همبستگی نسبی بین X و Y به طور همزمان در دو گروه، هر دو تحت کنترل X و Y توسط W، با محدودیت برابری در محل.
- برای محاسبه همبستگی مربعات بین X و Y.
- ساخت سینتاکس برای آزمایش یک فرضیه الگوی برای همبستگی. این نحو شامل چند صفت داده چند روش مورد بحث می شود.
- برای آزمایش یک فرضیه الگوی برای ارتباط با مشتقات جزئی.
GROUP 1 bivariate correlation
DA NG=2 NI=2 NO=40
CM
0.958365
0.231046 1.163310
MO NX=2 NK=2 LX=DI,FR PH=ST TD=ZE
LK
X Y
ST .5 LX 1 1 LX 2 2 PH 2 1
PD
OU ME=ML ND=4 XM EP=0.00001 IT=1000 NS AD=OFF
GROUP 2 bivariate correlations
DA NI=2 NO=40
CM
0.923433
0.021623 1.263412
MO NX=2 NK=2 LX=DI,FR PH=ST TD=ZE
LK
X Y
ST .5 LX 1 1 LX 2 2 PH 2 1
EQ PH(1,2,1) PH(2,1)
PD
OU ME=ML ND=4 XM EP=0.00001 IT=1000 NS AD=OFF
TI partial correlation
DA NI=3 NO=40
CM
1.405466
0.633555 0.958365
0.359973 0.231046 1.163310
MO NX=3 NK=3 LX=FU,FI PH=SY,FI TD=ZE
LK
W X Y
FR PH 1 1 PH 3 2 LX 2 1 LX 2 2 LX 3 1 LX 3 3
VA 1 PH 2 2 PH 3 3 LX 1 1
ST .5 PH 1 1 PH 3 2 LX 2 1 LX 2 2 LX 3 1 LX 3 3
PD
OU ME=ML ND=4 XM EP=0.00001 IT=1000 NS AD=OFF
GROUP 1 partial correlation
DA NG=2 NI=3 NO=65
CM
1.371222
0.308131 0.875000
0.063412 0.024306 0.085601
MO NX=3 NK=3 LX=FU,FI PH=SY,FI TD=ZE
LK
W X Y
FR PH 1 1 PH 3 2 LX 2 1 LX 2 2 LX 3 1 LX 3 3
VA 1 PH 2 2 PH 3 3 LX 1 1
ST .5 PH 1 1 PH 3 2 LX 2 1 LX 2 2 LX 3 1 LX 3 3
PD
OU ME=ML ND=4 XM EP=0.00001 IT=1000 NS AD=OFF
GROUP 2 partial correlation
DA NI=3 NO=49
CM
1.593040
0.104162 1.034864
0.043919 0.123677 0.086420
MO NX=3 NK=3 LX=FU,FI PH=SY,FI TD=ZE
LK
W X Y
FR PH 1 1 PH 3 2 LX 2 1 LX 2 2 LX 3 1 LX 3 3
VA 1 PH 2 2 PH 3 3 LX 1 1
ST .5 PH 1 1 PH 3 2 LX 2 1 LX 2 2 LX 3 1 LX 3 3
EQ PH(1,3,2) PH(3,2)
PD
OU ME=ML ND=4 XM EP=0.00001 IT=1000 NS AD=OFF
TI corr_squared
DA NI=2 NO=40
CM
0.958365
0.231046 1.163310
MO NX=2 NK=2 LX=FU,FI PH=SY,FI TD=ZE AP=1
LK
X Y
FR LX 1 1 LX 2 2 PH 2 1
ST .5 LX 1 1 LX 2 2 PH 2 1
VA 1 PH 1 1 PH 2 2
CO PA(1)=PH(2,1)**2
PD
OU ME=ML ND=4 XM EP=0.00001 IT=1000 NS AD=OFF
TI bivariate correlation pattern hypothesis
DA NI=6 NO=113
CM
1.00
0.53 1.00
0.56 0.44 1.00
0.65 0.38 0.40 1.00
0.42 0.52 0.30 0.56 1.00
0.40 0.31 0.53 0.56 0.40 1.00
MO NX=6 NK=6 LX=DI,FR PH=ST TD=ZE
LK
QS AS ES QP AP EP
ST .5 LX 1 1 LX 2 2 LX 3 3 LX 4 4 LX 5 5 LX 6 6
ST .5 PH 2 1 PH 3 1 PH 3 2 PH 4 1 PH 4 2 PH 4 3
ST .5 PH 5 1 PH 5 2 PH 5 3 PH 5 4 PH 6 1 PH 6 2 PH 6 3 PH 6 4 PH 6 5
EQ PH 2 1 PH 5 1 PH 4 2 PH 5 4
EQ PH 3 1 PH 6 1 PH 4 3 PH 6 4
EQ PH 3 2 PH 6 2 PH 5 3 PH 6 5
PD
OU ME=ML ND=4 XM EP=0.00001 IT=1000 NS AD=OFF
TI partial correlation pattern hypothesis
DA NI=10 NO=1071
CM
0.249
0.003 0.229
0.025 0.157 0.283
0.032 0.141 0.213 0.258
-0.006 0.146 0.143 0.134 0.223
0.024 0.171 0.269 0.217 0.178 0.377
0.017 0.137 0.201 0.181 0.143 0.248 0.283
-0.009 0.146 0.144 0.128 0.166 0.172 0.149 0.246
0.028 0.178 0.278 0.231 0.180 0.342 0.257 0.195 0.459
0.012 0.143 0.194 0.174 0.146 0.231 0.203 0.166 0.275 0.316
MO NX=10 NK=10 LX=FU,FI PH=SY,FI TD=ZE
LK
SEX M08 R08 C08 M10 R10 C10 M12 R12 C12
FR PH 1 1 PH 3 2 PH 4 2 PH 4 3 PH 5 2 PH 5 3 PH 5 4 PH 6 2 PH 6 3
FR PH 6 4 PH 6 5 PH 7 2 PH 7 3 PH 7 4 PH 7 5 PH 7 6 PH 8 2 PH 8 3
FR PH 8 4 PH 8 5 PH 8 6 PH 8 7 PH 9 2 PH 9 3 PH 9 4 PH 9 5 PH 9 6
FR PH 9 7 PH 9 8 PH 10 2 PH 10 3 PH 10 4 PH 10 5 PH 10 6 PH 10 7
FR PH 10 8 PH 10 9 LX 2 1 LX 3 1 LX 4 1 LX 5 1 LX 6 1 LX 7 1 LX 8 1
FR LX 9 1 LX 10 1 LX 2 2 LX 3 3 LX 4 4 LX 5 5 LX 6 6 LX 7 7 LX 8 8
FR LX 9 9 LX 10 10
VA 1 PH 2 2 PH 3 3 PH 4 4 PH 5 5 PH 6 6 PH 7 7 PH 8 8 PH 9 9 PH 10 10
VA 1 LX 1 1
ST .5 PH 1 1 PH 3 2 PH 4 2 PH 4 3 PH 5 2 PH 5 3 PH 5 4 PH 6 2 PH 6 3
ST .5 PH 6 4 PH 6 5 PH 7 2 PH 7 3 PH 7 4 PH 7 5 PH 7 6 PH 8 2 PH 8 3
ST .5 PH 8 4 PH 8 5 PH 8 6 PH 8 7 PH 9 2 PH 9 3 PH 9 4 PH 9 5 PH 9 6
ST .5 PH 9 7 PH 9 8 PH 10 2 PH 10 3 PH 10 4 PH 10 5 PH 10 6 PH 10 7
ST .5 PH 10 8 PH 10 9 LX 2 2 LX 3 3 LX 4 4 LX 5 5 LX 6 6 LX 7 7 LX 8 8
ST .5 LX 9 9 LX 10 10
EQ PH 3 2 PH 6 5 PH 9 8
EQ PH 4 2 PH 7 5 PH 10 8
EQ PH 4 3 PH 7 6 PH 10 9
PD
OU ME=ML ND=4 XM EP=0.00001 IT=1000 NS AD=OFF
[1] Preacher, K. J. (2006). Testing complex correlational hypotheses using structural equation modeling. Structural Equation Modeling, 13, 520-543.
